Question

Find an equation of the plane passing through the point (0,0,6) perpendicular to x=1-t y=2+t z=4-2t

Answer 1

The equation of plane is x-y+z=12.

Explanation:

It is given that the plane passing through the point (0,0,6) perpendicular to x=1-t y=2+t z=4-2t.

The given line is perpendicular to required plane, so coefficients of t represents the normal vector.

Normal vector is

`\overrightarrow {n}=<-1,1,-2>`

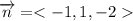
If a plane passes through
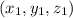`(x_1,y_1,z_1)` and having normal vector
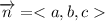`\overrightarrow {n}=<a,b,c>`, then the equation of plane is

`a(x-x_1)+b(y-y_1)+c(z-z_1)=0`

`-1(x-0)+1(y-0)+(-2)(z-6)=0`

`-x+y-2z+12=0`

`-x+y-2z=-12`

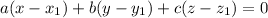
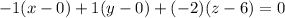
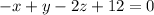
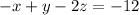
Multiply both sides by -1.

`x-y+2z=12`

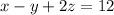
Therefore, the equation of plane is x-y+z=12.