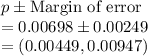Question

In a clinical​ study, 4300 healthy subjects aged​ 18-49 were vaccinated with a vaccine against a seasonal illness. Over a period of roughly 28​ weeks, 30 of these subjects developed the illness. Complete parts a through e below.

a. Find the point estimate of the population proportion that were vaccinated with the vaccine but still developed the illness. The point estimate is nothing. ​(Round to five decimal places as​needed.)b. Find the standard error of this estimate. The standard error of this estimate is nothing. ​(Round to five decimal places as​needed.)c. Find the margin of error for a 95​% confidence interval. The margin of error is nothing. ​(Round to five decimal places as​needed.)d. Construct the 95​% confidence interval for the population proportion. Interpret the interval. The 95​% confidence interval for the population proportion is (__,__). ​

Answer 1

a) 0.00698

b) 0.00127

c) 0.00249

d) (0.00449,0.00947)

Explanation:

We are given the following in the question:

Number of people vaccinated, n = 4300

Number of subjects that developed illness after vaccination, x = 30

a) point estimate of the population proportion that were vaccinated with the vaccine but still developed the illness.

`p = \displaystyle(x)/(n) = (30)/(4300) = 0.00698`

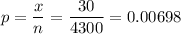
b) standard error of this estimate

`\text{Standard error} = \sqrt{\displaystyle(pq)/(n)} = \sqrt{\displaystyle(p(1-p))/(n)} = \sqrt{\displaystyle(0.00698* 0.99302)/(4300)} = 0.00127`

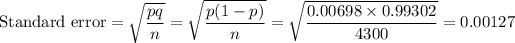
c) margin of error for a 95​% confidence interval

`z_(critical)\text{ at}~\alpha_(0.05) = 1.96`

`\text{Margin of error} = z_\text{critical}* \text{Standard error}\\= \pm 1.96* 0.00127 = \pm 0.00249`

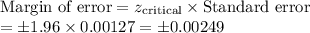
d) 95​% confidence interval

`p\pm \text{Margin of error}\\= 0.00698\pm 0.00249\\=(0.00449,0.00947)`