Answer:
The value of ΔE for the combustion reaction -4,955.76 kJ/mol.
Step-by-step explanation:
Heat released by the reaction = Heat absorbed by the calorimeter + Heat absorbed by the water
![q=[q_1+q_2]](https://img.qammunity.org/2021/formulas/chemistry/high-school/8jsgl8vo1kxujuj5pb849b4ka49s47k2kw.png)
![-q=[c_1* \Delta T+m_2* c_2* \Delta T]](https://img.qammunity.org/2021/formulas/chemistry/high-school/l677w90wucsgi7t3oda61xc33tobuxvqog.png)
where,
q = heat released by the reaction
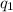 = heat absorbed by the calorimeter
= heat absorbed by the calorimeter
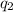 = heat absorbed by the water
= heat absorbed by the water
 = specific heat of calorimeter =
= specific heat of calorimeter =

 = specific heat of water =
= specific heat of water =
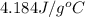
 = mass of water =
= mass of water =
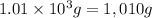
 = change in temperature = 27.20 °C - 24.70 °C =2.5°C
= change in temperature = 27.20 °C - 24.70 °C =2.5°C
Now put all the given values in the above formula, we get:
![-q=[(867 J/^oC* 2.5 ^oC)+(1,010* 4.184J/g^oC* 2.5^oC)]](https://img.qammunity.org/2021/formulas/chemistry/high-school/8jy5piwkxbz2nbjd1njotoubimtbqzy832.png)
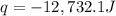
Now we have to calculate the enthalpy change for combustion reaction

where,
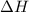 = enthalpy change = ?
= enthalpy change = ?
q = heat released = -12,732.1 J = -12.7321 kJ
n = moles of nonanedioic acid
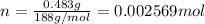
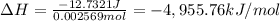
The value of ΔE for the combustion reaction -4,955.76 kJ/mol.