Question

Examine the diagram and information to answer the question.

AABC has vertices at A(3,4), B(-1, 1), and C(-2,5).

What is the approximate perimeter of AABC?
14.2 units
68 units
8.2 units
15 units

Answer 1

Perimeter of ΔABC is approximately equal to 14.2 units.

Explanation:

Given:

A = (3,4)

B = (-1,1)

C =(-2,5)

We need to find the perimeter of ΔABC.

Solution We will first find the length of each side.

length of each side can be cal calculated by using distance formula of geometry which gives.

`s = √((x_2-x_1)^2+(y_2-y_1)^2)`

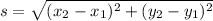
Where;

s⇒ Length of the line.

By Using this formula we will find the length of each side.

Length of side AB =
`√(((-1)-3)^2+(1-4)^2)= √((-4)^2+(-3)^2)=√(16+9)=√(25) = 5\ units`

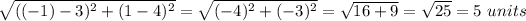
Length of side BC =
`√(((-2)-(-1)^2+(5-1)^2)= √((-1)^2+(4)^2)=√(1+16)=√(17) = 4.1\ units`

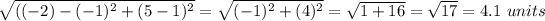
Length of side CA =
`√(((3)-(-2)^2+(4-5)^2)= √((5)^2+(-1)^2)=√(25+1)=√(26) = 5.1\ units`

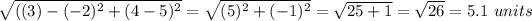
Now Perimeter of the triangle is given sum of all sides.

Perimeter of ΔABC = AB + BC + CA = 5 + 4.1 + 5.1 = 14.2 units

Hence Perimeter of ΔABC is approximately equal to 14.2 units.