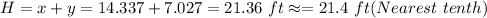Question

A person is standing 50 ft from a statue. The person looks up at an angle of elevation of

16° when staring at the top of the statue. Then the person looks down at an angle of
depression of 8° when staring at the base of the statue. How tall is the statue to the
nearest tenth of a foot?

Answer 1

The height of the statue is 21.4 feet.

Explanation:

Given:

Distance of the person from the statue = 50 ft

Angle of elevation of the top of statue = 16°

Angle of depression of the bottom of statue = 8°

The diagram is drawn below.

In triangle ABC:

BC = 50 ft, ∠ABC = 16°

Using trigonometric formula;

`\tan(16)=(y)/(50)`

`y=50\tan(16)`

`y=14.337\ ft`

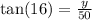
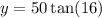
Now, let us determine the height of man, 'x'.

Consider triangle BDE.

ED = 50 ft, ∠BDE = 8°

Using trigonometric formula;

`\tan(8)=(x)/(50)\\\\x=50\tan(8)\\\\x=7.027\ ft`

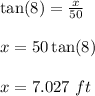
Now, from the diagram, it is clear that, height of statue is given as:

`H=x+y=14.337+7.027=21.36\ ft\approx=21.4\ ft(Nearest\ tenth)`