Question

The tape in a video tape cassette has a total length 212 m and can play for 2.1 h. As the tape starts to play, the full reel has an outer radius of 45 mm and an inner radius of 11 mm. At some point during the play, both reels will have the same angular speed, what is this common angular speed ? Answer in units of rad/s.

Answer 1

The common angular speed of the reels is 1 rad/s.

Step-by-step explanation:

Given:

Total length of the tape (d) = 212 m

Total time of run (t) = 2.1 hours

1 hour = 3600 s

So, 2.1 hours = 2.1 × 3600 = 7560 s

So, total time of run (t) = 7560 s

Inner radius (r) = 11 mm = 0.011 m

Outer radius (R) = 45 mm = 0.045 m

Now, linear speed of the tape (v) =
`(d)/(t)=(212)/(7560)=0.028\ m/s`

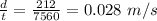
Let the same angular speed be
`\omega`.

Now, average radius of the reel is given as the sum of the two radii divided by 2.

So, average radius is,
`R_(avg)=(R+r)/(2)=(0.045+0.011)/(2)=(0.056)/(2)=0.028\ m`

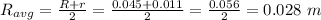
Now, common angular speed is given as the ratio of linear speed and average radius of the tape. So,

`\omega=(v)/(R_(avg))\\\\\\\omega=(0.028)/(0.028)\\\\\\\omega=1\ rad/s`

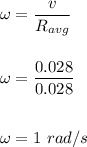
So, the common angular speed of the reels is 1 rad/s.