Question

For each of the following equations.

Find the coordinates of the vertex of the curve it describes.
Find the x− intercepts.
Find the y− intercept.
Find the equation of the line of symmetry.
Use all this information to sketch the graph of the function.

y= 1 4 (8x−x2)

Answer 1

Part 1) The vertex is the point (4,4)

Part 2) The x-intercepts are the points (0,0) and (8,0)

Part 3) The y-intercept is the point (0,0)

Part 4) The equation of the line of symmetry is x=4

Part 5) The graph in the attached figure

Explanation:

The correct quadratic equation is

`y= (1)/(4)(8x-x^(2))`

Part 1) Find the coordinates of the vertex

we have

`y= (1)/(4)(8x-x^(2))`

This is a vertical parabola open down (leading coefficient is negative)

The vertex is a maximum

Convert to vertex form

Factor -1

`y= -(1)/(4)(x^(2)-8x)`

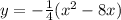
Complete the square

`y= -(1)/(4)(x^(2)-8x+16))+4`

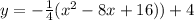
Rewrite as perfect squares

`y= -(1)/(4)(x-4)^(2)+4` ----> equation in vertex form

The vertex is the point (4,4)

Part 2) Find the x-intercepts

Remember that

The x-intercepts are the values of x when the value of y is equal to zero

so

For y=0

`-(1)/(4)(x-4)^(2)+4=0`

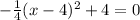
solve for x

Multiply both sides by 4

`(x-4)^(2)=16`

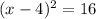
square root both sides

`x-4=\pm4\\x=4\pm4\\x=4+4=8\\x=4-4=0`

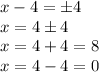
therefore

The x-intercepts are the points (0,0) and (8,0)

Part 3) Find the y-intercept

Remember that

The y-intercept is the value of y when the value of x is equal to zero

so

For x=0

`y= -(1)/(4)(0-4)^(2)+4`

`y= -4+4=0`

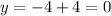
therefore

The y-intercept is the point (0,0)

Part 4)

Find the equation of the line of symmetry

we know that

In a vertical parabola the equation of the line of symmetry is equal to the x-coordinate of the vertex

The vertex is the point (4,4)

so

The equation of the line of symmetry is x=4

Part 5) Graph the function

we have

The vertex is the point (4,4)

The x-intercepts are the points (0,0) and (8,0)

The y-intercept is the point (0,0)