Question

G(t)=−(t−1)^2+5

Over which interval does g have an average rate of change of zero?


Choose 1 answer:


(Choice A)


1≤t≤4


(Choice B)


−4≤t≤−3


(Choice C)


−2≤t≤0


(Choice D)


−2≤t≤4

Answer 1

In the interval of - 2 ≤ t ≤ 4, the average rate of change is zero.

Explanation:

The function is given to be
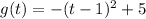`g(t) = - (t - 1)^(2) + 5` ............ (1)

(i) Now, for 1 ≤ t ≤ 4, we will put t = 1 and t = 4.

So, g(1) = 5, g(4) = - 4. {From equation (1)}

Hence, g(1) ≠ g(4)

(ii) Now, for - 4 ≤ t ≤ - 3, we will put t = - 4 and t = - 3.

So, g(- 4) = - 20, g(- 3) = - 11. {From equation (1)}

Hence, g(- 4) ≠ g(- 3)

(iii) Now, for -2 ≤ t ≤ 0, we will put t = - 2 and t = 0.

So, g(- 2) = - 4, g(0) = 4. {From equation (1)}

Hence, g(- 2) ≠ g(0)

(iv) Now, for - 2 ≤ t ≤ 4, we will put t = - 2 and t = 4.

So, g(- 2) = - 4, g(4) = - 4. {From equation (1)}

Hence, g(- 2) = g(4)

Therefore, in the interval of - 2 ≤ t ≤ 4, the average rate of change is zero. (Answer)