Question

Help me out guys. Got stuck over this algebra question ​

Answer 1

Compare LHS and RHS to prove the statement.

Explanation:

Given: a + b + c = 0

We have to show that
`$ (1)/(1 + x^b + x^(-c)) + (1)/(1 + x^c + x^(-a)) + (1)/(1 + x^a + x^(-b)) = 1$`

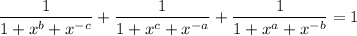
We take LCM, simplify the terms and compare LHS and RHS. We will see that LHS = RHS and the statement will be proved.

Taking LCM, we get:

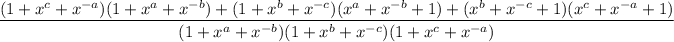`$ ((1 + x^c + x^(-a))(1 + x^a + x^(-b)) + (1 + x^b + x^(-c))(x^a + x^(-b) + 1) + (x^b + x^(-c) + 1)(x^c + x^(-a) + 1))/((1 + x^a + x^(-b))(1 + x^b + x^(-c))(1 + x^c + x^(-a)))  $` = 1

⇒
`(1 + x^c + x^(-a))(1 + x^a + x^(-b)) + (1 + x^b + x^(-c))(x^a + x^(-b) + 1) + (x^b + x^(-c) + 1)(x^c + x^(-a) + 1)   = (1 + x^a + x^(-b))(1 + x^b + x^(-c))(1 + x^c + x^(-a))`

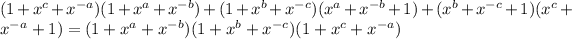
We simplify each term and then compare LHS and RHS.

Simplifying the first term:

`(1 + x^c + x^(-a))(1 + x^a + x^(-b))`

=
`$ x^(c + a) + x^(c - b) + x^c +  1 + x^(-a - b) + x^(-a) + x^(a) + x^(-b) + 1 $`

=
`$ x^(c + a) + x^(c - b) + x^(c) + x^(-a - b) + x^(-a) + x^(a) + x^(-b) + 2  \hspace{5mm} \hdots (A)$`

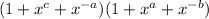
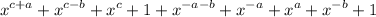
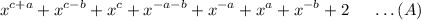
Now, we simplify the second term we have:

`$ (1 + x^b + x^(-c))(x^a + x^(-b) + 1)  $`

=
`$ x^(a + b) + 1 + x^(b) + x^(a - c) + x^(-b - c) + x^(-c) + x^(a) + x^(-b) + 1 $`

=
`$ x^(a + b) + x^(b) + x^(a - c) + x^(- c - b) + x^(-c) + x^a + x^(-b) + 2 \hspace{5mm} \hdots (B) $`

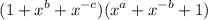
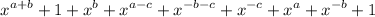
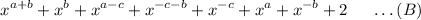
Again, simplifying
`(x^b + x^(-c) + 1)(x^c + x^(-a) + 1)`,

=
`$x^(b + c) + x^(b - a) + x^b + 1 + x^(-c -a) + x^(-c) + x^c + x^(-a) + 1 $`

=
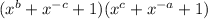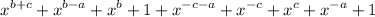
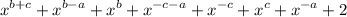`$ x^(b + c) + x^(b - a) + x^b + x^(-c -a) + x^(-c) + x^c + x^(-a) + 2 $`(C)

Therefore, LHS = A + B + C

=
`$ x^(c + a) + x^(c - b) + 2x^c + x^(-a - b) + 2x^(-a) + 2x^(a) + 2x^(-b) + x^(a + b) + 2x^b + x^(a - c) + x^(-c -b) + x^(b + c) + x^(b - a) + x^(-c -a) + 6 $`

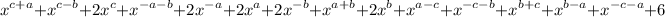
Similarly. RHS

=
`$ (x^(b + c) + x^(b - a) + x^b + 1 + x^(-c -a) + x^(-c) + x^c + x^(-a) + 1)(x^a + x^(-b) + 1) $`

Note that if a + b + c = 0,
`$ \implies x^(a + b + c) = x^0 = 1 $`

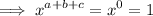
So, RHS =
`x^(c + a) + x^(c - b) + 2x^c + x^(-a - b) + 2x^(-a) + 2x^(a) + 2x^(-b) + x^(a + b) + 2x^b + x^(a - c) + x^(-c -b) + x^(b + c) + x^(b - a) + x^(-c -a) + 6`

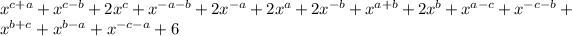
We see that LHS = RHS.

Therefore, the statement is proved.