Question

37. ABC has vertices A(0, 0) , B(0, 4) , and C(3, 0) . Write the equation for the line containing the altitude overline AR in standard form

Answer 1

3x - 4y = 0

Explanation:

The triangle Δ ABC has vertices A(0,0), B(0,4) and C(3,0).

Therefore, the equation of the straight line BC in intercept form will be

`(x)/(3) + (y)/(4) = 1`

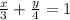
⇒ 4x + 3y = 12

⇒
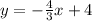`y = - (4)/(3)x + 4` .......... (1)

This is a equation in slope-intercept form and the slope is
`- (4)/(3)`.

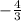Now, the altitude AR is perpendicular to equation (1) and hence its slope will be
`(3)/(4)`.

{Since, the product of slope of two mutually perpendicular straight line is always - 1}

Therefore, the equation of the altitude AR which passes through A(0,0) will be

`y = (3)/(4)x`

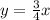
⇒ 4y = 3x

⇒ 3x - 4y = 0 (Answer)