Question

Given: LP=NP
ML=MN
Prove: LQ=QN

Answer 1

The Proof is below.

Explanation:

Given:

`\overline {LP} \cong \overline{NP}`

`\overline {ML} \cong \overline{MN}`

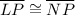
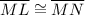
To Prove:

`\overline {LQ} \cong \overline{QN}`

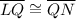
Proof:

In ΔLPM and ΔNPM

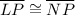`\overline {LP} \cong \overline{NP}` ……….{Given}

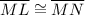`\overline {ML} \cong \overline{MN}` ……….{Given}

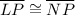`\overline {LP} \cong \overline{NP}` ……….{Reflexive Property}

ΔLPM ≅ ΔNPM ….{ By Side-Side-Side congruence test}

∴ ∠LMP ≅ ∠NMP ...{Corresponding parts of congruent triangles (c.p.c.t).}.....( 1 )

Now In ΔLMQ and ΔNMQ

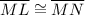`\overline {ML} \cong \overline{MN}` ……….{Given}

∠LMQ ≅ ∠NMQ ..........{From 1 above}

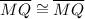`\overline {MQ} \cong \overline{MQ}` ……….{Reflexive Property}

ΔLMQ ≅ ΔNMQ ....{ By Side-Angle-Side Congruence test}

∴
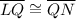`\overline {LQ} \cong \overline{QN}` ...{Corresponding parts of congruent triangles (c.p.c.t).}.....Proved