Question

I'm not sure where to begin

Answer 1

∠B = 28°,
`a = 69.61\ and\ c = 56.87`

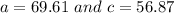
Explanation:

Given:

A triangle ABC with the following data:

∠A = 98°, ∠C = 54°, b = 33

Now, for a triangle, the sum of all interior angles is equal to 180°. So,

∠A + ∠B + ∠C = 180°

⇒ 98° + ∠B + 54° = 180°

⇒ ∠B + 152° = 180°

⇒ ∠B = 180° -152°

⇒ ∠B = 28°

Now, using the sine rule for a triangle, we can find the remaining sides of the triangle. The sine rule is:

`(\sin A)/(a)=(\sin B)/(b)=(\sin C)/(c)\\\\(\sin 98\°)/(a)=(\sin 28\°)/(33)\\\\a=(33* \sin 98\°)/(\sin 28\°)\\\\a=69.61`

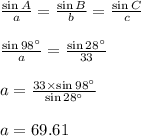
Now, we consider the second pair of fraction.

`(\sin B)/(b)=(\sin C)/(c)`

`(\sin 28\°)/(33)=(\sin 54\°)/(c)\\\\c=(33*\sin 54\°)/(\sin 28\°)\\\\c=56.87`

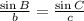
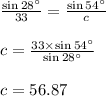
Therefore, the missing data are:

∠B = 28°, a = 69.61 and c = 56.87