Question

Ellie has a delivery van which she is going to deliver boxes each box is a cuboid brain.ly 45cm by 40cm by 35cm the space in the van is empty and by has maximum length 3.6m maximum width 1.6m maximum height of 2.1m Ellie wants to put as many boxes possible in the van she can put 3 boxes in the van in 1 minute how many minutes will it take ellie to put as many boxes in a van as possibe

Answer 1

It will take Ellie 64 minutes to put as many boxes as possible.

Explanation:

Let us work with meters.

The dimensions of Ellie's boxes in meters are: 0.45m by 0.40m by 0.35 ( to convert from centimeters to meters we just divide by 100, because 1m =100cm). therefore the volume of each box is:

`V_(box)=0.45m*0.40m*0.35m=0.063m^3`

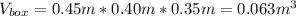
Now the dimensions of the empty van are 3.6m by 1.6m by 2.1 m, therefore its volume
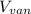`V_(van)` is:

`V_(van)=3.6m*1.6m*2.1m=12.096m^3.`

So the amount of boxes that Ellie can put in the van is equal to the volume of the van
`V_(van)` divided by the volume
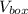`V_(box)` of each box:

`(V_(van))/(V_(box)) =(12.096)/(0.063)=\boxed{192\:boxes }`

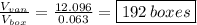
So 192 boxes can be put into the van.

Now Ellie can put 3 boxes in the van in 1 minute, therefore the amount of time it will take her to put 192 boxes into the van will be:

`(192boxes)/(3boxes/minute) =\boxed{64\:minutes}`

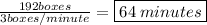
So it takes Ellie 64 minutes to put as many boxes into the van as she can.