Question

A rectangle has one side of 8 cm. How fast is the diagonal of the rectangle changing at the instant when the other side is 6 cm and increasing at 3 cm per minute?

Answer 1

The diagonal is increasing at 1.8 cm/minute.

Explanation:

Let l be one side,w be other side and s be diagonal.

We have

s² = l² + w²

We have

l = 8 cm

w = 6 cm

s² = l² + w²

s² = 8² + 6²

s² = 100

s = 10 cm

Taking derivative with respect to time in s² = l² + w²

`s^2=l^2+w^2\\\\2s(ds)/(dt)=2l(dl)/(dt)+2w(dw)/(dt)\\\\s(ds)/(dt)=l(dl)/(dt)+w(dw)/(dt)\\\\(dw)/(dt)=3cm/min\\\\(dl)/(dt)=0cm/min\\\\10(ds)/(dt)=8* 0+6* 3\\\\(ds)/(dt)=1.8cm/min`

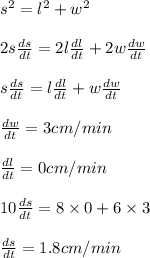
The diagonal is increasing at 1.8 cm/minute.