Question

A. find the critical points of the following function on the given interval

B. Use a graphing utility to determine whether the critical points correspond to local maxima, and local minima, or neither.

C. Find the absolute maximum and minimum values on the given interval.

f(theta)=sin(theta)+4 cos(theta); [-2pi,2pi]

Identify all the critical points.

Identify all the critical points that are local minima.

Answer 1

A) Given function:

`f(\theta)=sin(\theta)+4cos(\theta)`

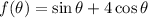
to determine the critical points we need to differentiate
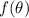`f(\theta)` and equate it to zero. (the slopes of the curve at the critical point is always zero)

`(d)/(d\theta)(f(\theta))=(d)/(d\theta)(sin(\theta)+4cos(\theta))`

`(f'(\theta)=cos(\theta)-4sin(\theta)`

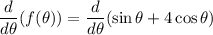
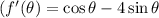
now use
`(f'(\theta)=0`

`0=cos(\theta)-4sin(\theta)`

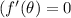
now solve for
`\theta` within the range
`[-2\pi,2\pi]`

`4sin(\theta)=cos(\theta)`

`(sin(\theta))/(cos(\theta))=(1)/(4)`

`tan(\theta)=(1)/(4)`

`\theta=\arctan\left({(1)/(4)\right)}`

`\alpha=0.2450`

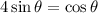
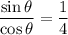
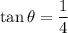
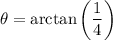
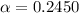
as positive tan lies in the first and third quadrant of the unit-circle. our values within the interval
`[-2\pi,2\pi]` will be:

`\begin{tabular}{ccccc}\theta=&-2\pi+\alpha,&-\pi+\alpha,&0+\alpha,&\pi+\alpha&\theta=&-2\pi+0.2450,&-\pi+0.2450,&0.2450,&\pi+0.2450&\theta=&-6.038,&-2.897,&0.2450,&3.38,\end{tabular}\\`

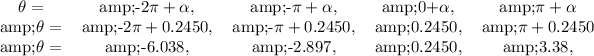
These are the critical points!

We can use these values to find the values of
`f(\theta)`

B) From the graph we can see that the first and third are maxima and second and fourth are minima.

C) Since all minimum points have the same y-coordinate, and all maximum points have the same y-coordinate. We can safely say that all points are local critical points in this function.