Answer:
c. 6.5 seconds.
Explanation:
We have been given that a a paper plane is thrown from the top of a 147-foot cliff into the water below, the height of the plane at any given time can be determined by the formula
 , where h is the height of the plane at t seconds.
, where h is the height of the plane at t seconds.
To find the time, when plane will be at a height of exactly 20.25 feet, we will substitute
 in our given formula and solve for t as:
in our given formula and solve for t as:
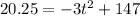
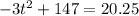
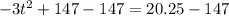
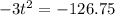
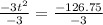
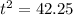
Take square root of both sides:
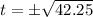
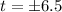
Since time cannot be negative, therefore, the plane will be at a height of exactly 20.25 feet after 6.5 seconds and option 'c' is the correct choice.