Question

Consider a random sample of x1,. . . , xn from a uniform distribution U(0, θ) with unknown parameter θ, where θ > 0.

Determine the maximum likelihood estimator of θ.

Answer 1

`\hat \theta = max (X_1,...,X_n)`

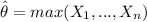
Explanation:

We assume the following density function:

`f(\theta) = (1)/(\theta) , 0 \leq x\leq \theta`

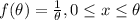
And 0 for other case, and we are interested in order to find the MLE for
`\theta`

The likehood function would have the following form:

`L(\theta) = \prod_(i=1)^n f(x_i) = (1)/(\theta^n),0\leq x_i \leq \theta , i=1,...,n`

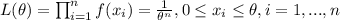
If we want to maximize this we need a value
`\theta` such that
`\theta\geq x_i` for
`i =1,....,n`

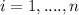
Our likehood function is a decreasing function and in order to estimate this value we can use the maximum function of all the observations:

`\theta = max (x_1,....,x_n)`

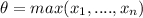
And the the MLE estimator for the parameter
`\theta` is given by
`\hat \theta = max (X_1,...,X_n)`

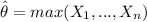
Is important to mention that this estimator probably underestimate the value of
`\theta` since
`max (X_1,...,X_n)< \theta`, but is the stimator for this case.