Answer:
b. 21.4 % (nearest tenth)
Explanation:
P(lose) = 33% = 0.33
P(win) = 1 - 0.33 = 0.67
Using binomial distribution X ~ B(n, p)
where n is the number of trials and p is the probability of success
⇒ X ~ B(15, 0.67)
Binomial probability formula:
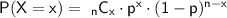


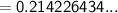
Converting to percentage:
0.214266434... x 100% = 21.4 % (nearest tenth)