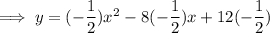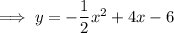Answer:
(a)

(b)
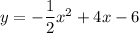
Explanation:
(a) From inspection of the graph, the x-intercepts (where
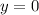 ) are at
) are at
 and
and
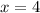 .
.
Therefore
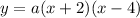 where
where
 is some constant
is some constant
The y-intercept is at (0, -8)
Expanding the equation:
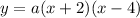
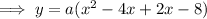
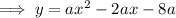
Therefore, -8a is the y-intercept
Comparing y-intercepts: -8 = -8a ⇒ a = 1
Substituting a = 1, the final equation in standard form is:

--------------------------------------------------------------------------------------------------
(b) From inspection of the graph, the x-intercepts (where
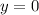 ) are at
) are at
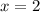 and
and
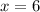 .
.
Therefore
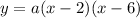 where
where
 is some constant
is some constant
The y-intercept is at (0, -6)
Expanding the equation:
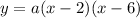

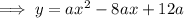
Therefore, 12a is the y-intercept
Comparing y-intercepts:
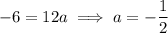
Substituting found value of a into the equation: