To solve this problem we must apply the concept related to the longitudinal effort and the effort of the hoop. The effort of the hoop is given as
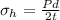
Here,
P = Pressure
d = Diameter
t = Thickness
At the same time the longitudinal stress is given as,
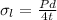
The letters have the same meaning as before.
Then he hoop stress would be,
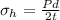
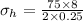
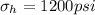
And the longitudinal stress would be
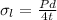
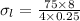
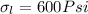
The Mohr's circle is attached in a image to find the maximum shear stress, which is given as
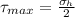

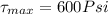
Therefore the maximum shear stress in the pressure vessel when it is subjected to this pressure is 600Psi