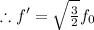Question

A meter stick swinging from one end oscillates with a frequency f0. What would be the frequency, in terms of f0 , if the bottom half of the stick were cut off?

Answer 1

Answer: f = √2(f0)

Step-by-step explanation:

For a swing, the frequency function can be written as

f0 = 1/2π √(mgl/i)

Where f0 = frequency, m = mass, g = acceleration due to gravity,

Therefore for the length

f0 = 1/2π√(g/L)

Where L = length

When the length is cut by half, L = L/2

Substituting L with L/2 we have;

f = 1/2π√(g/(L/2))

f = 1/2π√(2g/L)

f = √2/2π√(2g/L)

f = √2×f0

f = √2(f0)

Answer 2

To solve this problem we will proceed to define the Period of a stick, then we will define the frequency, which is the inverse of the period. We will compare the change suffered by the new length and replace that value. The Time period of meter stick is

`T = 2\pi\sqrt{ (L)/(g)}`

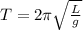
Here,

L = Length

g = Gravity

At the same time the frequency is

`f = (1)/(T)`

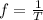
Therefore the frequency in Terms of the Period is

`f_0 = (1)/(2\pi)\sqrt{(g)/(L)}`

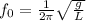
If bottom third were cut off then the new length is

`L' = (2)/(3) L`

Replacing this value at the new frequency we have that,

`f ' = (1)/(2\pi) \sqrt{(3g)/(2L)}`

`f' = \sqrt{(3)/(2)}((1)/(2\pi)\sqrt{(g)/(L)})`

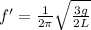
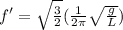
Finally,

`\therefore f' = \sqrt{(3)/(2)}f_0`