Question

An apartment complex can rent all 200 of its one-bedroom apartments at a monthly rate of $600. For each $20 increase in rent, 4 additional apartments are left unoccupied. At what monthly rate should each apartment be rented in order to maximize the total rent collected?

Answer 1

The monthly rate should each apartment be rented is $ 800 in order to maximize the total rent collected

Solution:

Given that apartment complex can rent all 200 of its one-bedroom apartments at a monthly rate of $600

For rent:

Given that rent at monthly rate is $ 600

Also, For each $20 increase in rent, 4 additional apartments are left unoccupied

Therefore, for a given rent x,

Rent ⇒ 600 + 20x ( here plus sign denotes increase in rent)

Rooms ⇒ 200 - 4x ( here minus sign denotes 4 additional apartments are left unoccupied)

Now total revenue is given as:

R = (600 + 20x)(200 - 4x)

`R = 120000 -2400x + 4000x - 80x^2`

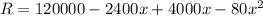
For maximum total rent to be collected,

`(dR)/(dx) = 0`

Differentiate R with respect to x

`0 - 2400 + 4000 - 160x = 0\\\\-160x = -1600\\\\x = 10`

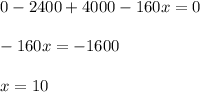
To find the rate of each apartment be rented in order to maximize the total rent collected is:

Rent = 600 + 20x = 600 + 20(10) = 600 + 200 = $ 800

Thus monthly rate should each apartment be rented is $ 800