Question

Use the graph of f(x) = |(x^2 − 4)(x^2 + 2)| to find how many numbers in the interval [0, 1] satisfy the conclusion of the Mean Value Theorem.

Answer 1

2 numbers will satisfy the mean value theorem in the interval [0, 1]

View Image

Explanation:

The Mean Value Theorem states that if f(x) is continuous at every point in a closed interval [a, b], and is differentiable at every point of its interior (a, b), then at least one point c in interval (a, b) that satisfy the equation:

`f'(c)=(f(b)-f(a))/(b-a)`

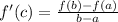
Or simply put it, at some point in the graph, the instantaneous rate of change (the derivative) will equal the average rate of change (
`(y_2-y_1)/(x_2-x_1)`).

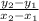If you remember, a derivative is just the slope, which is how much the function is increasing or decreasing. So, whenever there is a change in curvature, the slope is changing from positive to negative. Each curvature will have a new set of slopes.

It's hard to explain, but basically, each additional curve the graph has means there's an additional point where the derivative will equal the average slope. So every new curve means an additional number that will satisfy the mean value theorem.

In this problem, I graphed out the function f(x) = |(x² − 4)(x² + 2)| on the interval [0, 1]. You can see that there's 2 curves so there'll be 2 numbers that will satisfy the mean value theorem.

I drew some visuals in the picture below.

• The green line is the average rate of change
  `((y_2-y_1)/(x_2-x_1))`.
• The green dots are the instantaneous rate of change (the derivative).