Question

When rolling two standard six-sided dice, what is the probability that the sum of the dice will be even or a multiple of 3? (show your work)

Answer 1

Probability that the sum of the dice will be even or a multiple of 3 is
`(5)/(6)`

Solution:

Given that two standard six sided dice are rolled

To find: probability that the sum of the dice will be even or a multiple of 3

The probability of an event is given as:

`probability =\frac{\text { number of favorable outcomes }}{\text { total number of possible outcomes }}`

Let us first find probability that the sum of dice will be even

The total possible outcomes when two dice are rolled is:

{ (1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6) }

total number of possible outcomes = 36

Here,

favorable outcome = sum of dice is even

favorable outcome = (1, 1) , (1, 3) , (1, 5) , (2, 2) , (2, 4) , (2, 6) , (3, 1) , (3, 3) , (3, 5) , (4, 2) , (4, 4) , (4, 6) , (5, 1) , (5, 3) , (5, 5) , (6, 2) , (6, 4) , (6 , 6)

Therefore, number of favorable outcomes = 18

Therefore,

`p(sum\ is\ even) = (18)/(36)`

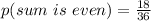
Let us first find probability that the sum of dice is multiple of 3

favorable outcome = sum of dice is multiple of 3

favorable outcome = (1, 2) , (1 , 5) , (2 , 1 ) , (2, 4) , (3 , 3) , (3 , 6) , (4 , 2) , (4 , 5) , (5 , 1) , (5 , 4) , (6 , 3) , (6 , 6)

Therefore, number of favorable outcomes = 12

Thus probability is given as:

`p(\text{ sum is multiple of 3}) = (12)/(36)`

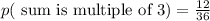
Total probability that the sum of the dice will be even or a multiple of 3:

total probability = p( sum is even ) + p(sum is multiple of 3)

`\rightarrow (18)/(36) + (12)/(36) = (18+12)/(36)\\\\\rightarrow (30)/(36) = (5)/(6)`

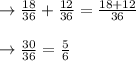
Thus probability that the sum of the dice will be even or a multiple of 3 is
`(5)/(6)`