Question

Choose the equivalent system of linear equations that will produce the same solution as the one given below. (1 point) 4x − 2y = 6 2x + y = 5

Answer 1

Bro did the most^ its D

Answer 2

Question:

Choose the equivalent system of linear equations that will produce the same solution as the one given below.

4x - 2y = 6

2x + y = 5

Options:

A) -4x - 2y = 10

-4y = 4

B) -4x - 5y = -1

-7y = 5

C) 3x + 2y = 6

7x = 12

D) 4x + 2y = 10

8x = 16

Answer:

Option D

The equivalent system of linear equations that will produce the same solution as the one given is 4x + 2y = 10 and 8x = 16

Solution:

Given system of equations are:

4x - 2y = 6 --------- eqn 1

2x + y = 5 ------- eqn 2

Multiply eqn 2 by 2

2(2x + y = 5)

4x + 2y = 10 --------- eqn 3

Add eqn 1 and eqn 3

4x - 2y + 4x + 2y = 6 + 10

8x = 16

x = 2

Substitute x = 2 in eqn 1

4(2) - 2y = 6

8 - 2y = 6

2y = 8 - 6

2y = 2

y = 1

Thus the solution of given system of equations is (x , y) = (2, 1)

Let us check the options one by one

Option A)

Given system of equations are:

-4x - 2y = 10 ---- eqn 1

-4y = 4 --- eqn 2

Substitute the obtained solution (x, y) = (2, 1) in above equations and check if it makes the equation true

From eqn 2,

-4(1) = 4

`-4\\eq 4`

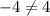
Thus this option does not produce the same solution as the one given

Option B)

-4x - 5y = -1 ----- eqn 1

-7y = 5 ------- eqn 2

Substitute the obtained solution (x, y) = (2, 1) in above equations and check if it makes the equation true

From eqn 2,

`-7(1) = 5\\\\-7\\eq 5`

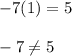
Thus this option does not produce the same solution as the one given

Option C)

3x + 2y = 6 ------ eqn 1

7x = 12 --------- eqn 2

Substitute the obtained solution (x, y) = (2, 1) in above equations and check if it makes the equation true

From eqn 2,

`7(2) = 12\\\\14\\eq 12`

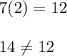
Thus this option does not produce the same solution as the one given

Option D)

4x + 2y = 10 ------ eqn 1

8x = 16 -------- eqn 2

Substitute the obtained solution (x, y) = (2, 1) in above equations and check if it makes the equation true

From eqn 2,

8(2) = 16

16 = 16

Also,

from eqn 2,

8x = 16

x = 2

substitute x = 2 in eqn 1

4(2) + 2y = 10

8 + 2y = 10

2y = 2

y = 1

Thus solution is (2, 1)

Thus this option produce the same solution as the one given