Question

The driver of a car traveling at 23.1 m/s applies the brakes and undergoes a constant

deceleration of 1.03 m/s^2.

How many revolutions does each tire makebefore the car comes to a stop, assuming that the car does not skid and that the tires have​ radii of 0.33 m?
Answer in units of rev.

Answer 1

The tires make 125 revolutions before the car stops

Step-by-step explanation:

Circular and Linear Motion

A tire rotates around a fixed point and the tire when in contact with the ground, drives a vehicle in a linear path. This is an example of a relationship between both types of movements that can be taking place simultaneously.

The car is moving with an initial speed of
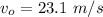`v_o=23.1\ m/s` and then breaks at
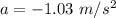`a=-1.03\ m/s^2` until it stops. We can compute the time take to stop by using

`\displaystyle v_f=v_o+a.t`

Solving for t

`\displaystyle t=(v_f-v_o)/(a)`

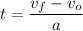
Putting in numbers

`\displaystyle t=(0-23.1)/(-1.03)`

`\displaystyle t=22.427\ sec`

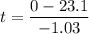
Now, let's transfer this information to the circular motion. We know the tangent speed is

`\displaystyle v_t=w.r`

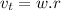
Being w the angular speed and r the radius of the circle, in this case, the tires. The tangent speed is the same as the speed of motion of the car. It gives us the initial angular speed

`\displaystyle w_o=(v_t)/(r)`

`\displaystyle w_o=(23.1)/(0.33)=70\ rad/s`

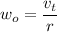
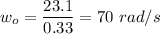
When the circular motion is not uniform, i.e. there is angular acceleration
`\alpha`, the angular speed is a function of time

`\displaystyle w=w_o+\alpha t`

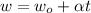
We can compute the angular acceleration knowing the final angular speed is zero when the car stops.

`\displaystyle \alpha=(w-w_o)/(t)=(0-70)/(22.427)`

`\displaystyle \alpha=-3.121\ rad/s^2`

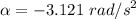
The rotation angle is also a function of time as shown

`\displaystyle \theta=w_o\ t+(\alpha t^2)/(2)`

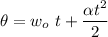
Using the given and computed values

`\displaystyle =70(22.427)-(3.121(22.427)^2)/(2)`

`\displaystyle \theta =784.95\ rad`

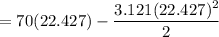
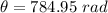
Knowing each revolution is
`2\pi` radians, the number of revolutions is

`\displaystyle n=(\theta )/(2\pi)=125\ rev`

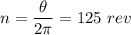
The tires make 125 revolutions before the car stops