Question

This diagram shows a pre-image △ABC , and its image, ​ △A′′B′′C′′ ​ , after a series of transformations. Select from the drop-down menus to correctly complete the statements. △ABC is to become △A′B′C′ . Then ​ △A′B′C′ ​ is to become ​ △A′′B′′C′′ ​ . Because the transformations are , the pre-image and image are . Triangles on a coordinate plane whose axes are labeled x and y. Triangle A B C has vertex A at negative 2 comma 1, vertex B at negative 5 comma negative 2, and vertex C at negative 3 comma negative 4. Triangle A prime B prime C prime has vertex A prime at 2 comma 1, vertex B prime at 5 comma negative 2, and vertex C prime at 3 comma negative 4. Triangle A double prime B double prime and C double prime has vertex A double prime at negative 1 comma 2, vertex B double prime at 2 comma 5, and vertex C double prime at 4 comma 3.

Answer 1

1. reflected across the y-axis

2.rotated 90 degrees counterclockwise about the origin

3.both rigid

4.congruent

Explanation:

hope this helps!

Answer 2

1. Reflection across the y-axis

2. Rotation over the origin by 90° in anticlockwise direction

Explanation:

Triangle ABC has vertices A(-2,1), B(-5,-2) and C(-3,-4).

1) Reflect this triangle across the y-axis. This reflection has the rule:

`(x,y)\rightarrow (-x,y)`

Thus,

• 
  `A(-2,1)\rightarrow A'(2,1);`
• 
  `B(-5,-2)\rightarrow B'(5,-2);`
• 
  `C(-3,-4)\rightarrow C'(3,-4).`

2) Rotate triangle A'B'C' over the origin by 90° in anticlockwise direction. This rotation has the rule:

`(x,y)\rightarrow (-y,x)`

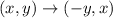
So,

• 
  `A'(2,1)\rightarrow A''(-1,2);`
• 
  `B'(5,-2)\rightarrow B''(2,5);`
• 
  `C'(3,-4)\rightarrow C''(4,3).`