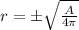Question

A= 4 πr^2 solve for R

Answer 1

`r = \pm\sqrt{(A)/(4 \pi)}`

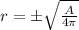
Explanation:

Given:

The given equation is
`A = 4 \pi r^(2)`

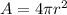
We need to solve the given equation for r.

Rewrite the equation as.

`4 \pi r^(2)=A`

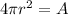
Divide both side of the equation by 4π and simplify

`(4 \pi r^(2))/(4 \pi)=(A)/(4 \pi)`

`r^(2)=(A)/(4 \pi)`

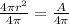
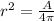
Take the square root both side of the equation.

`\sqrt{r^(2) } = \sqrt{(A)/(4 \pi)}`

`r = \pm\sqrt{(A)/(4 \pi)}`

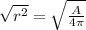
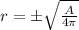
Therefore, the solution for r is both positive or negative
`r = \pm\sqrt{(A)/(4 \pi)}`