Question

30. You are designing a survey to determine the proportion of voters who support mandatory handgun registration. You intend to generate a 95% confidence interval for this value and want the margin of error to be no more than .025. If you had no idea what the true population proportion was, how many more people would you need to survey than if you thought the true population proportion was very close to .3?(A) 175(B) 1537(C) 535(D) 322(E) 246

Answer 1

Answer: (E) 246

Explanation:

Formula to find the sample size :

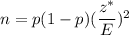`n=p(1-p)((z^*)/(E))^2` , where p= Prior estimate of population proportion, z^*= Critical z-value and E = margin of error .

Let p be the Prior proportion of voters who support mandatory handgun registration..

As per given, we have

E= 0.025

Critical z value for 95% confidence level =z*=1.96

If p=0.30

Required sample size would be :

`n=(0.30)(1-0.30)((1.96)/(0.025))^2`

`n=(0.21)(78.4)^2`

`n=1290.7776\approx1291`

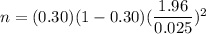
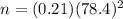
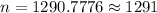
If no Prior proportion is known , then we take p= 0.50

Required sample size =
`n_0=(0.50)(1-0.50)((1.96)/(0.025))^2`

`=1536.64\approx1537`

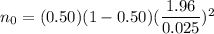
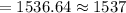
Difference :
`n_0-n=1537-1291=246`

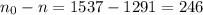
∴ If we had no idea what the true population proportion was, we need 246 more people to survey than if you thought the true population proportion was very close to .3.

Therefore , the correct answer is (E) 246 .