Question

A force is applied to the rim of a disk that can rotate like a merry-go-round, so as to change its angular velocity. Its initial and final angular velocities, respectively, for four situations are the following.

(a) -2 rad/s, 5 rad/s;
(b) 2 rad/s, 5 rad/s;
(c) -2 rad/s, -5 rad/s; and
(d) 2 rad/s, -5 rad/s.

Rank the situations according to the work done by the torque due to the force, greatest first.

Answer 1

The work done by the torque is the same in each case.

Step-by-step explanation:

Work-Energy Theorem can be used to calculate the work done by the torque in each case.

`W = \Delta K\\W = K_2 - K_1 = (1)/(2)I\omega_2^2 - (1)/(2)I\omega_1^2\\`

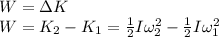
Let's apply this theorem to each case:

`W_a = (1)/(2)I(5)^2 - (1)/(2)I(-2)^2 = (1)/(2)I(21)\\W_b = (1)/(2)I(5)^2 - (1)/(2)I(2)^2 = (1)/(2)I(21)\\W_c = (1)/(2)I(-5)^2 - (1)/(2)I(-2)^2 = (1)/(2)I(21)\\W_d = (1)/(2)I(-5)^2 - (1)/(2)I(2)^2 = (1)/(2)I(21)`

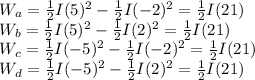
As can be seen from the results, in each case the work done by the torque is the same.