Question

For a hypothesis comparing two population means, H0: μ1 ≤ μ2, what is the critical value for a one-tailed hypothesis test, using a 5% significance level, with both sample sizes equal to 13? Assume the population standard deviations are equal. Select one: a. +1.401 b. +1.711 c. +2.060 d. +2.064

Answer 1

D. +2.064

Explanation:

Total number of samples = 13+13 =26, degree of freedom = 26 - 2 = 24

t-value (critical value) corresponding to 24 degrees of freedom and 0.05 significance level is +2.064

Answer 2

"=T.INV(0.95,24)" and we got
`t_(crit)=+1.711`

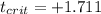
b. +1.711

Explanation:

When we have two independent samples from two normal distributions with equal variances we are assuming that

`\sigma^2_1 =\sigma^2_2 =\sigma^2`

And the statistic is given by this formula:

`t=\frac{(\bar X_1 -\bar X_2)-(\mu_(1)-\mu_2)}{S_p\sqrt{(1)/(n_1)+(1)/(n_2)}}`

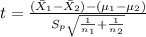
Where t follows a t distribution with
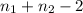`n_1+n_2 -2` degrees of freedom and the pooled variance
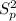`S^2_p` is given by this formula:

`\S^2_p =((n_1-1)S^2_1 +(n_2 -1)S^2_2)/(n_1 +n_2 -2)`

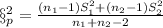
This last one is an unbiased estimator of the common variance
`\sigma^2`

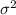
The system of hypothesis on this case are:

Null hypothesis:
`\mu_1 \leq  \mu_2`

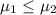
Alternative hypothesis:
`\mu_1 > \mu_2`

Or equivalently:

Null hypothesis:
`\mu_1 - \mu_2 \leq 0`

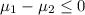
Alternative hypothesis:
`\mu_1 -\mu_2 > 0`

Our notation on this case :

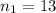`n_1=13` represent the sample size for group 1

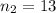`n_2 =13` represent the sample size for group 2

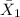`\bar X_1` represent the sample mean for the group 1

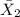`\bar X_2` represent the sample mean for the group 2

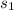`s_1` represent the sample standard deviation for group 1

`s_2` represent the sample standard deviation for group 2

Now we can calculate the degrees of freedom given by:

`df=13+13-2=24`

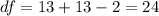
Since is a right tailed test we need to look on the t distribution with 24 degrees of freedom that accumulates 0.05 of the area on the right. And we can use the following excel code:

"=T.INV(0.95,24)" and we got
`t_(crit)=+1.711`

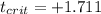
b. +1.711