Question

An engineer designed a valve that will regulate water pressure on an automobile engine. The engineer designed the valve such that it would produce a mean pressure of 7.8 pounds/square inch. It is believed that the valve performs above the specifications. The valve was tested on 26 engines and the mean pressure was 8.1 pounds/square inch with a standard deviation of 0.9. A level of significance of 0.05 will be used. Assume the population distribution is approximately normal. Determine the decision rule for rejecting the null hypothesis. Round your answer to three decimal places.

Answer 1

Null hypothesis is not rejected.

Explanation:

We are given that the engineer designed the valve such that it would produce a mean pressure of 7.8 pounds/square inch. It is believed that the valve performs above the specifications. So,

Null Hypothesis,
`H_0` :
`\mu` <= 7.8 {means that the valve designed by the engineer produce a mean pressure less than or equal to 7.8 pounds/square inch}

Alternate Hypothesis,
`H_1` :
`\mu` > 7.8 {means that the valve designed by the engineer produce a mean pressure more than 7.8 pounds/square inch}

The test statistics used here will be;

T.S. =
`(Xbar -\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

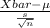where, X bar = sample mean pressure = 8.1 pounds/square inch

s = sample standard deviation = 0.9

n = sample of engines = 26

So, test statistics =
`(8.1 -7.8)/((0.9)/(√(26) ) )` ~
`t_2_5`

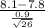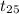
= 1.699

Decision Rule : If the critical value of t table is less than the test statistics, then we will reject null hypothesis.

And If the critical value of t table is more than the test statistics, then we will not reject null hypothesis.

Now, at 5% level of significance t table gives critical value of 1.708 .Since our test statistics is less than the critical value so we have insufficient evidence to reject null hypothesis.

Therefore, we conclude that the valve designed by the engineer does not produce a mean pressure of more than 7.8 pounds/square inch .

Answer 2

Answer with explanation:

Let
`\mu` be the population mean.

As per given , we have

`H_0: \mu=7.8`

`H_a: \mu>7.8`

Since population variance is not known and alternative hypotheis sis right tailed , so we perform a right-tailed t-test.

Test statistic :
`t=\frac{\overline{x}-\mu}{(s)/(√(n))}`

, where n= sample size

`\overline{x}` = Sample mean

s= sample standard deviation.

As per given ,

n=26

`\overline{x}=8.1`

s=0.9

Put these values in formula we get

`t=(8.1-7.8)/((0.9)/(√(26)))`

`t=(0.3)/((0.9)/( 5.099))`

`t=1.69967\approx1.700`

For significance level of 0.05 and degree of freedom df=25 (df = n-1),

The right tailed critical t-value = t^*= 1.708 (By t-table)

Decision rule : Reject
`H_0` when
`t_(cal)>t^*(1.708)` .

Since the calculated t value(1.700) is less than the critical value ( 1.708) , we are failed to reject null hypothesis.

We conclude that the valve does not perform above the specifications.