Question

The common electrical wall receptacle voltage in North America is often referred to as 120 volts AC. One hundred twenty volts is: O the average voltage over many weeks of time. O the peak voltage from an AC wall receptacle. O the arithmetic mean of the voltage as it varies with time. O one-half the peak voltage. O the root mean square (rms) average of the voltage as it varies with time.

Answer 1

120 volts is the root mean square (rms) average of the voltage as it varies with time.

Step-by-step explanation:

A. The average voltage over many weeks of time (false)

Reason: Average AC voltage over one cycle is cycle (from one peak to other) is zero and so over many weeks of time it is zero.

B. The peak voltage from an AC wall receptacle (false)

Reason: The peak voltage of an AC source in North America is zero.

C. The arithmetic mean of the voltage as it varies with time (false)

Reason: Arithmetic mean AC voltage over one cycle is cycle (from one peak to other) is zero and so over many weeks of time it is zero.

D. One-half the peak voltage (false)

Peak voltage =170 Volts

One-half the peak voltage = 85 volts

E. The root mean square (rms) average of the voltage as it varies with time (True)

Reason:

The peak voltage and root mean square voltage are related by:

`V_(rms)=(V_(p))/(√(2) )\\\\V_(rms)=\frac{170}√(2)V_(rms)\\\\V_(rms)=120 Volts`

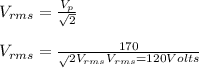
Average value of voltage over one cycle is zero, so instead of calculating average voltage for AC peak voltage is first squared and the mean is calculated.