Question

If x = 3 is a zero of the polynomial function f(x) = 2x3 + x2 − 25x + 12, which of the following is another zero of f(x)?a. x = -3b. x = 4c. x = -4d. x = 12

Answer 1

-4

Explanation:

Answer 2

b)
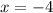`x=-4` is another zero of the polynomial

Explanation:

Since you are given a set of options to choose from, a very simple way to find the zero of the polynomial is by simply plugging each value from the options and seeing which of them gives the answer 0.

`f(x) = 2x^3+x^2-25x+12\\`

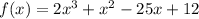
Using all the options:

`a)\,f(-3) = 2(-3)^3+(-3)^2-25(-3)+12\\f(-3) = 42\\\\b)\,f(4) = 2(4)^3+(4)^2-25(4)+12\\f(4) = 56\\\\c)\,f(-4) = 2(-4)^3+(-4)^2-25(-4)+12\\f(-4) = 0\\\\d)\,f(12) = 2(12)^3+(12)^2-25(12)+12\\f(12) = 3312`

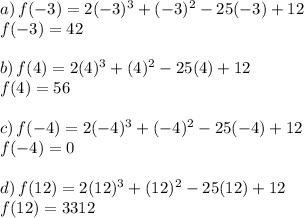
Now we know that at x = -4 the value of the polynomial f(x) is 0. hence

b)
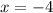`x=-4` is another zero of the polynomial