Answer:
 by angle-angle-side (
by angle-angle-side (
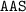 .)
.)
Explanation:
Let
 denote the radius of this circle.
denote the radius of this circle.
Notice that
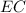 and
and
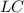 are each a radius of this circle. (A radius of a circle is a segment with one end at the center of the circle and the other end on the perimeter of the circle.)
are each a radius of this circle. (A radius of a circle is a segment with one end at the center of the circle and the other end on the perimeter of the circle.)
Therefore, the length of both segment
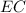 and segment
and segment
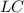 should be equal to the radius of this circle:
should be equal to the radius of this circle:
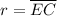 .
.
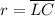 .
.
Therefore,
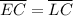 .
.
Thus,
 by angle-angle-side (
by angle-angle-side (
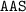 ) since:
) since: