Answer:
D. 15
Explanation:
For this case we can begin finding the number of ways in order to select two different books for Monday and Wednesday. We know that Jill can select a book on Monday in six different ways snce she has a total of 6 books. And for Wednesday, she need another book so then can select any of the five remaining books, and the total number of ways would be:
N= 6 × 5 = 30 ways.
We are going to assume that the order no matter. If she select a book A and then another B is the same if she select first the book B and then the book A. We are interested inthe possible pairs, and if the order no matter then the total possible pairs are:
Pairs = 30 / 2 = 15
So then the best answer would be D. 15
We can also find the solution using combinations. We have a total of 6 nooks, and we want to select two so then we hav C(6, 2) ways to select two. We need to remember that the formula for combinatories is given by:

Where
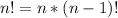
And if we replace the values we got this:
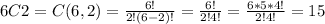
And as we can see we got the same solution from the previous part.