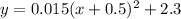Answer:
The equation of parabola in vertex form is
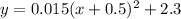
Explanation:
Given coordinate of vertex is
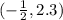 and the parabola passes through the point
and the parabola passes through the point
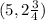
So, the equation of parabola in vertex form is

Where
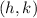 is the coordinate of the vertex.
is the coordinate of the vertex.
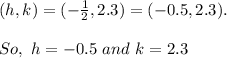
Plugging these value in equation we get,
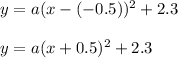
Now, we will find the value of

Plug the coordinate
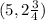
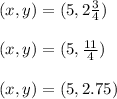
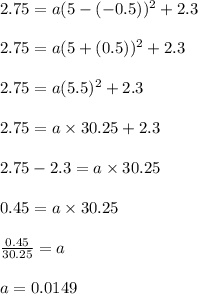
Plug the value of
 in the equation
in the equation
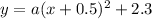
So, the equation of parabola with vertex
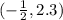 and passes through the point
and passes through the point
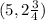 is
is
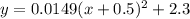 ≅
≅