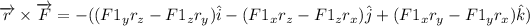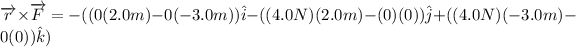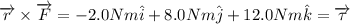Question

In unit-vector notation, what is the torque about the origin on a particle located at coordinates (0 m, −3.0 m, 2.0 m) due to force F with arrow 1 with components F1x = 4.0 N and F1y = F1z = 0

Answer 1

The torque about the origin is
`2.0Nm\hat{i}-8.0Nm\hat{j}-12.0Nm\hat{k}`

Step-by-step explanation:

Torque
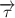`\overrightarrow{\tau}` is the cross product between force
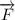`\overrightarrow{F}` and vector position
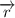`\overrightarrow{r}` respect a fixed point (in our case the origin):

`\overrightarrow{\tau}=\overrightarrow{r}*\overrightarrow{F}`

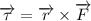
There are multiple ways to calculate a cross product but we're going to use most common method, finding the determinant of the matrix:

`\overrightarrow{r}*\overrightarrow{F} =-\left[\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k}\\ F1_(x) & F1_(y) & F1_(z)\\ r_(x) & r_(y) & r_(z)\end{array}\right]`

`\overrightarrow{r}*\overrightarrow{F} =-((F1_(y)r_(z)-F1_(z)r_(y))\hat{i}-(F1_(x)r_(z)-F1_(z)r_(x))\hat{j}+(F1_(x)r_(y)-F1_(y)r_(x))\hat{k})`

`\overrightarrow{r}*\overrightarrow{F} =-((0(2.0m)-0(-3.0m))\hat{i}-((4.0N)(2.0m)-(0)(0))\hat{j}+((4.0N)(-3.0m)-0(0))\hat{k})`

`\overrightarrow{r}*\overrightarrow{F}=-2.0Nm\hat{i}+8.0Nm\hat{j}+12.0Nm\hat{k}=\overrightarrow{\tau}`