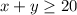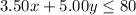Question

Jonah is going to the store to buy candles for his igloo. Small candles cost $3.50 and large candles cost $5.00. He needs to buy at least 20 candles, and he cannot spend more than $80.

Write a system of linear inequalities that represent the situation.

Answer 1

`x+y\geq 20`

`3.50x+5.00y\leq 80`

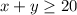
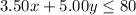
Explanation:

Let x represent number of small candles and y represent number of large candles.

We have been given that Jonah needs to buy at least 20 candles. This means number of small and large candles should be greater than or equal to 20. We can represent this information in an inequality as:

`x+y\geq 20...(1)`

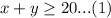
We are also told that small candles cost $3.50, so cost of x small candles would be
`3.50x`.

Since large candles cost $5.00, so cost of y large candles would be
`5.00y`.

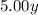We are told that Jonah cannot spend more than $80, this means cost of x small candles and y large candles should be less than or equal to $80. We can represent this information in an inequality as:

`3.50x+5.00y\geq 80`

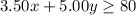
Therefore, our required system of inequalities would be:

`x+y\geq 20`

`3.50x+5.00y\leq 80`