Question

PLEASE HELP!!!!

Use spherical coordinates to find the volume of the region bounded by the sphere ρ=42cos(φ) and the hemisphere ρ=21, z≥0

How do you find the volume of a sphere ρ=42cos(φ)?
V = 4/3πr^3

Answer 1

We can rewrite the sphere's equation in Cartesian coordinates.

`\rho = 42 \cos(\varphi) \implies \rho^2 = 42 \rho \cos(\varphi) \implies x^2+y^2+z^2 = 42z`

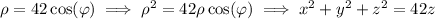
Complete the square to get

`x^2 + y^2 + z^2 - 42z = 0 \implies x^2 + y^2 + (z - 21)^2 = 21^2`

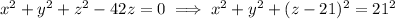
which represents a sphere centered at (0, 0, 21) with radius 21. You can find the sphere's volume easily from here.

But that's not what you're asked to do. You want to find the volume of the intersection of the two spheres. (see attached plot)

The two spheres meet in the plane z = 21/2:

`x^2+y^2+z^2 = 21^2 \implies x^2+y^2 = 21^2 - z^2`

`x^2+y^2+(z-21)^2 = 21^2 \implies 21^2 - z^2 + (z-21)^2 = 21^2 \implies z = \frac{21}2`

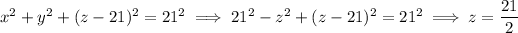
and we express this plane in spherical coordinates as

`z = \rho \cos(\varphi) = \frac{21}2 \implies \rho = \frac{21}2 \sec(\varphi)`

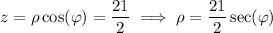
We use this plane to cut the region of interest in half; we have to do this to find the volume because the ρ coordinate does not vary uniformly between the two spheres. On the plus side, the region is symmetrical across this plane, so we only need one integral.

Find the angle φ at which the two spheres meet:

`42\cos(\varphi) = 21 \implies \cos(\varphi) = \frac12 \implies \varphi = \cos^(-1)\left(\frac12\right) = \frac\pi3`

Putting everything together, the volume of the region is

`\displaystyle 2 \int_0^(2\pi) \int_0^(\pi/3) \int_(21/2 \, \sec(\varphi))^(21) \rho^2 \sin(\varphi) \, d\rho \, d\varphi \, d\theta = \boxed{\fraC{15,435\pi}4}`

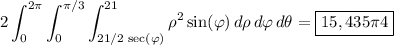
I leave the details of computation to you.