Question

Meth Barie's ice cream shop wants to decide whether to introduce a new ice cream flavor. They randomly selected 15 customers at their downtown Denton location to rate this new flavor. The rating is on a scale of 1 to 5, with 1 being not interested' and 5 being 'strongly interested. Meth Barie's will approve the new flavor if the true mean rating is over 4.0 1. What is the Alternative hypothesis for testing whether the new ice cream should be approved? A. Ha: μ s 4.0 C. Ha: μ 240 E. Ha: μ < 4.0 B.Ha: μ . 4.0 D. Ha: μ > 4.0 2. If the survey shows that the average rating is 4.4 with a standard deviation of 1.6, what is the calculated value of the test statistic? C. 1936 E.0.605 B. 0968 D. 0175 A. t 1.341 C. t 1.282 B.t>1.345D. t>1.761 3 What is the rejection region for testing at the 0.1 level of significance? E. t 0.1

Answer 1

Meth Barie's ice cream shop should not introduce the new ice cream flavor.

Explanation:

We are given the following in the question:

Population mean, μ = 4.01

Sample mean,
`\bar{x}` = 4.4

Sample size, n = 15

Alpha, α = 0.1

Sample standard deviation, s = 1.6 minutes

First, we design the null and the alternate hypothesis

`H_(0): \mu \leq 4.01\\H_A: \mu > 4.01`

We use one-tailed t test to perform this hypothesis.

Formula:

`t_(stat) = \displaystyle\frac{\bar{x} - \mu}{(s)/(√(n)) }`

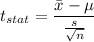
Putting all the values, we have

`t_(stat) = \displaystyle(4.4 - 4.0)/((1.6)/(√(15)) ) = 0.968`

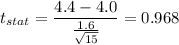
Option B) 0.968

Rejection region:

Now,
`t_(critical) \text{ at 0.10 level of significance, 9 degree of freedom } = 1.345`

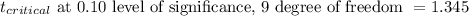
So the rejection region would be a value of t-statistic greater than 1.345.

Option B) t > 1.345

Conclusion:

Since,

`t_(stat) < t_(critical)`

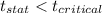
We fail to reject the null hypothesis and accept the null hypothesis. Meth Barie's ice cream shop should not introduce the new ice cream flavor.