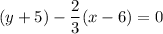Answer:
Option 4:
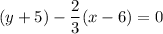
Explanation:
It is given that the line parallel to
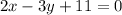
hence the slope of this line will the same as the slope of the line that we have to find.
to find the slope of the line, we just to rearrange it in the form y= mx+b
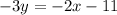
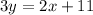
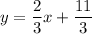
by comparing it to
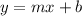 . we'll get that m = 2/3
. we'll get that m = 2/3
Now we have all that's needed to formulate the equation of our line.
- the point the line crosses (6,-5)
- the slope of the line
we'll use the general equation:
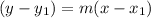 , here (x1,y1) = (6,-5)
, here (x1,y1) = (6,-5)
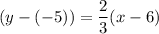

we see that this matches option 4.
with a little rearrangement this will be much clearer. We'll move everything on the left hand side of the equation.