Answer:
By 3 units is the interquartile range for Orlando's data set greater than the interquartile range for Victor's data set.
Explanation:
Given:
Victor's Data Set: {22, 29, 32, 27, 30}.
Orlando's Data Set: {36, 25, 33, 27, 35}.
Now, to find the units is the interquartile range for Orlando's data set greater than the interquartile range for Victor's data set.
So, we get the interquartile range of Victor's Data Set:
{22,27,29,30,32}
Q3 =

Q3 =
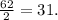
Q1 =
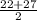
Q1 =
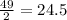
Thus, interquartile range is:
Interquartile range =

Interquartile range =
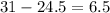
The interquartile range of Victor's Data Set = 6.5.
Now, to get the interquartile range of Orlando's Data Set:
{25,27,33,35,36}
Q1 =
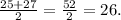
Q3 =
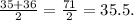
Thus, interquartile range is:
Interquartile range =

Interquartile range =
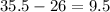
The interquartile range of Orlando's Data set = 9.5.
Now, to get the units of the interquartile range for Orlando's data set greater than the interquartile range for Victor's data set we subtract Victor's interquartile range from Orlando's interquartile range:
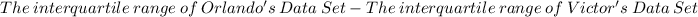
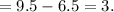
Therefore, by 3 units is the interquartile range for Orlando's data set greater than the interquartile range for Victor's data set.