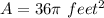Question

Please help! :)

The area of the shaded sector is 9 pi square feet.

A circle. A shaded sector has an angle measure of 90 degrees.

Which equation can be used to find the area of the entire circle, A?
StartFraction 9 pi over A EndFraction = StartFraction 90 degrees over 360 degrees EndFraction
StartFraction A over 9 pi EndFraction = StartFraction 90 degrees over 360 degrees EndFraction
StartFraction 9 pi over A EndFraction = StartFraction 180 degrees over 360 degrees EndFraction
StartFraction A over 9 pi EndFraction = StartFraction 180 degrees over 360 degrees EndFraction

Answer 1

1

Explanation:

Answer 2

So the correct option is First one

i.e
`(9\pi)/(A)=(90)/(360)`

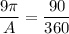
Explanation:

Given:

Area of Shaded part = 9 π square feet

To Find :

Area of Circle = ?

Solution:

90 degree center angle is equivalent to an area of 9 Π square feet

So, 360 degree center is equivalent to area A which is the area of the complete circle.

So the Ratio will be

`(90)/(9\pi) =(360)/(A)`

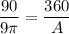
Setting the given statements in proportion:

`(90)/(9\pi) =(360)/(A)`

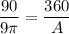
On solving we get the required

`(9\pi)/(A) =(90)/(360)`

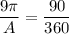
So the correct option is First one

i.e
`(9\pi)/(A)=(90)/(360)`

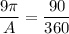
Alternate Method:

Shaded part is of 90°

Area of Shaded part = 9 π square feet

And Full Circle is of 360° that is 4 sector of 90°

`\textrm{Area of Circle}=4* (Shaded\ part)`

`\textrm{Area of Circle}=4* 9\pi`

`\textrm{Area of Circle}=36\pi`

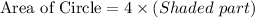
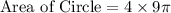
So the correct option is First one

i.e
`(9\pi)/(A)=(90)/(360)`

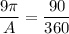
On solving this we get

`A=36\pi\ feet^(2)`