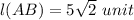Question

What is the distance between the points (-4, 2) and (1.-3) on the coordinate
plane?
ht

Answer 1

Therefore the distance between the points (-4, 2) and (1.-3) on the coordinate is

`l(AB) =5√(2)\ unit`

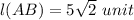
Explanation:

Given:

Let,

point A( x₁ , y₁) ≡ ( -4 , 2)

point B( x₂ , y₂ )≡ (1 , -3)

To Find:

`l(AB)=?`

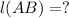
Solution:

We have Distance Formula between two point is given as

`l(AB) = \sqrt{((x_(2)-x_(1))^(2)+(y_(2)-y_(1))^(2) )}`

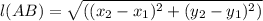
Substituting the given values we get

`l(AB) = \sqrt{((1--4)^(2)+(-3-2)^(2) )}`

`l(AB) = \sqrt{((1+4)^(2)+(-5)^(2) )}`

`l(AB) = √((25+25 ))=√(50)=5√(2)\ unit`

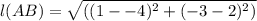
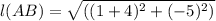
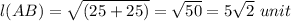
Therefore the distance between the points (-4, 2) and (1.-3) on the coordinate is

`l(AB) =5√(2)\ unit`