Question

Fred walked a trail at 2 mph. Paul started 30 minutes later on the same trail and walked at a pace of 3 mph. Create a system of equations in which y represents the distance walked in miles and x represents the time walked in hours. Explain what this solution means in terms of Paul catching up to Fred.

Answer 1

`y=2x\\y=3(x-(1)/(2))`

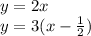
Paul will catch Fred after
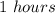`1\ hours` at a distance
`3\ miles`.

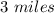Explanation:

Distance is represented by
`y` and the time is represented by
`x`. Here after
`x` hours(when Fred started) the distance covered by Fred and Paul is same that is
`y`.

For Fred:

time=
`x`

distance=
`y`

Speed
`=2\ mph`

`Distance=speed* time\\y=2* x \\y=2x`

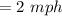
Paul:

Since Fred started 30 minutes earlier, so Paul's travel time will be 30 minutes less than that of Fred.

Time
`=x-(1)/(2)`

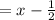
Speed
`=3\ mph`

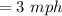
Distance
`=y\\`

`y=3* (x-(1)/(2))\\y=3(x-(1)/(2))`

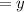
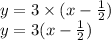
Hence system of equation

`y=2x\\y=3(x-(1)/(2))`

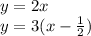
Solution of this system of equations gives the time, when Paul will catch Fred and distance covered by each of them.

`y=2x\\y=3(x-(1)/(2))\\\\2x=3x-(3)/(2)\\x=(3)/(2)\\\\y=2x\\y=2* (3)/(2)\\y=3`

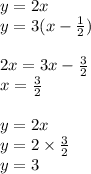
Time taken by Paul
`=x-(1)/(2)=(3)/(2)-(1)/(2)=1`

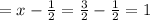
Hence Paul will catch Fred after
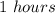`1\ hours` at a distance
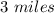`3\ miles`.