Question

What is the measure in degrees for the central angle of a circle whose radius is 9 cm and intercepted arc length is 7.2 cm?

Enter your answer as a decimal in the box, round your answer to the nearest hundredth.

Answer 1

Therefore the measure of the central angle is 45.86°.

Explanation:

Given:

Radius = 9 cm

arc length = 7.2 cm

pi = 3.14

To Find:

Central angle = θ =?

Solution:

If the θ measured in degree then the arc length is given as

`\textrm{arc lenght}=(\theta)/(360\°)* 2\pi r`

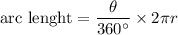
Where r = radius, θ = Central angle

On substituting the values we get

`7.2=(\theta)/(360)* 2* 3.14* 9\\\\\theta=(2592)/(56.52)=45.8598=45.86\\\therefore \theta=45.86\°`

Therefore the measure of the central angle is 45.86°.