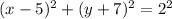Answer:
(a)
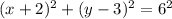
(b)
Explanation:
The standard form of circle is
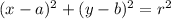
where, (a,b) is center and r is radius.
Properties of algebra:
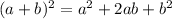
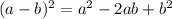
(a)
Consider the given equation is
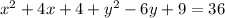
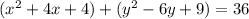
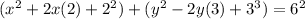
Using properties of algebra, we get
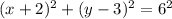
(b)
Consider the given equation is
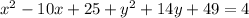
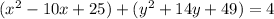
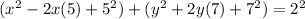
Using properties of algebra, we get