To solve this problem we will apply the linear motion kinematic equations. There we will find the acceleration, which will allow us to find the total displacement. From the relationship given between the circumference of a circle and the total length, we can determine the number of revolutions.
For the second part we will use the relationship between angular and linear velocities given through the radius of the circumference to calculate the final value.
PART A) Calculate the acceleration of the car

Where,
a = Acceleration
 = Initial velocity
= Initial velocity
v = Final velocity
t = time
Replacing we have that
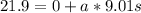

Calculate the displacement
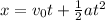
Replacing
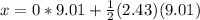
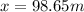
Calculate the circumference of wheel:
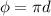
Where,
d = Diameter
 = Circumference
= Circumference
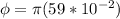
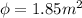
Calculate the number of revolutions
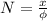
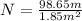
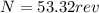
Therefore the number of revolutions is 53.32rev
PART B )
Calculate the angular velocity

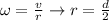
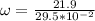
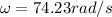
Therefore the final angular speed is 74.23rad/s