Question

2. Consider the circle x^2−4x+y^2+10y+13=0. There are two lines tangent to this circle having a slope of 2/3.

a. Find the coordinates of the two points of tangency.
b. Find the equations of the two tangent lines.

Answer 1

a) The coordinates are (0.431, -2.646) and (3.568,-7.354)

b) The tangent lines are

l₁ = (x-0.431)*2/3 - 2.646

l₂ = (x-3.568)2/3 - 7.354

Explanation:

First, lets complete squares, by taking for each cordinate the square of a linear expression

0= x²−4x+y²+10y+13 = (x-2)²+ 4 + (y+5)²-25+13 = (x-2)²+(y+5)² - 8

Hence (x-2)² + (y+5)² = 8

Lets put y in function of x. We should obtain 2 functions f and g that represent the circle.

(y+5)² = 8 - (x-2)² = -x² + 4x + 4

`y = ^+_- √(-x^2+4x+4) -5`

Thus

`f(x) = √(-x^2+4x+4) - 5`

`g(x) = -√(-x^2+4x+4) - 5`

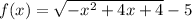
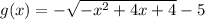
Lets find the derivate of each function and the points in which they reach the value 2/3. In those points the tangent line will have a slope of 2/3.

We may just find the values of x which the derivate of f is either 2/3 or -2/3.

`(-x+2)/(√(-x^2+4x+4)) = ^+_-(2)/(3) \Leftrightarrow (x^2-4x+4)/(-x^2+4x+4) = (4)/(9) \Leftrightarrow 9(x^2-4x+4) = 4(-x^2+4x+4) \\\Leftrightarrow 13x^2-52x+20 = 0`

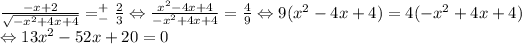
The quadratic has roots

`(52 ^+_-√(1664))/(26)`

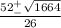
one root is 3.568, which corresponds with g, and the other root is 0.431, corresponding to f.

Also g(3.568) = - 7.354 and f(0.431) = -2.646

This means that the coordinates are (0.431 , -2.646), (3.568 , -7.354) and the tangent lines are

l₁ = (x-0.431)*2/3 - 2.646

l₂ = (x-3.568)2/3 - 7.354